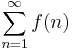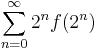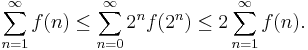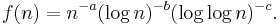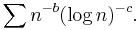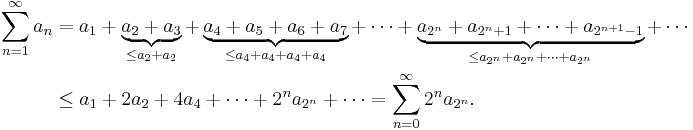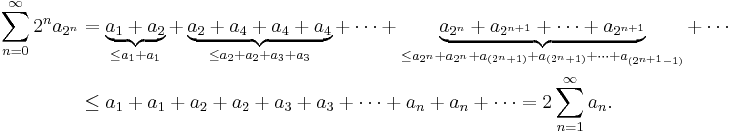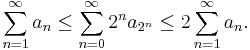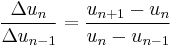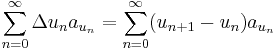Cauchy condensation test

In mathematics, the Cauchy condensation test, named after Augustin-Louis Cauchy, is a standard convergence test for infinite series. For a positive non-increasing sequence f(n), the sum

\sum_{n=1}^{\infty}f(n)

converges if and only if the sum

\sum_{n=0}^{\infty} 2^{n}f(2^{n})

converges. Moreover, in that case we have

\sum_{n=1}^{\infty}f(n) \leq \sum_{n=0}^{\infty} 2^{n}f(2^{n}) \leq 2 \sum_{n=1}^{\infty}f(n).

A geometric view is that we are approximating the sum with trapezoids at every 2^{n}. Another explanation is that, as with the analogy between finite sums and integrals, the 'condensation' of terms is analogous to a substitution of an exponential function. This becomes clearer in examples such as

\ f(n) = n^{-a} (\log n)^{-b} (\log \log n)^{-c}.

Here the series definitely converges for a > 1, and diverges for a < 1. When a = 1, the condensation transformation essentially gives the series

\sum n^{-b} (\log n)^{-c}.

The logarithms 'shift to the left'. So when a = 1, we have convergence for b > 1, divergence for b < 1. When b = 1 the value of c enters.

Contents

Proof

Let f(n) be a positive, non-increasing sequence of real numbers. To simplify the notation, we will write an = f(n). We are to investigate the series 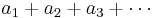a_1%2Ba_2%2Ba_3%2B\cdots. The condensation test follows from noting that if we collect the terms of the series into groups of lengths 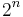2^{n}, each of these groups will be less than 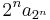2^{n} a_{2^{n}} by monotonicity. Observe,

\begin{align} \sum_{n=1}^{\infty} a_n & = a_1%2B\underbrace{a_2%2Ba_3}_{\leq a_2%2Ba_2}%2B\underbrace{a_4%2Ba_5%2Ba_6%2Ba_7}_{\leq a_4%2Ba_4%2Ba_4%2Ba_4}%2B\cdots %2B\underbrace{a_{2^n}%2Ba_{2^n%2B1}%2B\cdots %2Ba_{2^{n%2B1}-1}}_{\leq a_{2^n}%2Ba_{2^n}%2B\cdots %2Ba_{2^n}}%2B\cdots \\ & \leq a_1 %2B 2 a_2 %2B 4 a_4 %2B \cdots %2B 2^n a_{2^n} %2B \cdots = \sum_{n=0}^{\infty} 2^n a_{2^n}. \end{align}

We have used the fact that the sequence an is non-increasing, thus 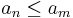a_n\leq a_m whenever 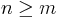n\geq m. The convergence of the original series now follows from direct comparison to this "condensed" series. To see that convergence of the original series implies the convergence of this last series, we similarly put,

\begin{align} \sum_{n=0}^{\infty} 2^n a_{2^n} & = \underbrace{a_1%2Ba_2}_{\leq a_1%2Ba_1}%2B\underbrace{a_2%2Ba_4%2Ba_4%2Ba_4}_{\leq a_2%2Ba_2%2Ba_3%2Ba_3}%2B\cdots %2B\underbrace{a_{2^n}%2Ba_{2^{n%2B1}}%2B\cdots %2Ba_{2^{n%2B1}}}_{\leq a_{2^n}%2Ba_{2^n}%2Ba_{(2^n%2B1)}%2Ba_{(2^n%2B1)}%2B\cdots %2Ba_{(2^{n%2B1}-1)}}%2B\cdots \\ & \leq a_1 %2B a_1 %2B a_2 %2Ba_2 %2B a_3 %2B a_3 %2B \cdots %2B a_n %2B a_n %2B \cdots = 2 \sum_{n=1}^{\infty} a_n. \end{align}

And we have convergence, again by direct comparison. And we are done. Note that we have obtained the estimate

\sum_{n=1}^{\infty} a_n \leq \sum_{n=0}^{\infty} 2^n a_{2^n} \leq 2 \sum_{n=1}^{\infty} a_n.

This proof is a generalization of Oresme's proof of the divergence of the harmonic series.

Generalizations

The following generalization is due to Schlömilch. Let 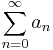\sum_{n=0}^{\infty} a_n be an infinite real series whose terms are positive and non-increasing, and let 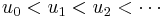u_0<u_1<u_2<\cdots be a strictly increasing sequence of positive integers such that

\frac{\Delta u_n}{\Delta u_{n-1}} = \frac{u_{n%2B1}-u_n}{u_n-u_{n-1}}

is bounded, where 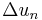\Delta u_n is the forward difference. Then the series 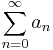\sum_{n=0}^{\infty} a_n converges if the series

\sum_{n=0}^{\infty} {\Delta u_n} a_{u_n} = \sum_{n=0}^{\infty} (u_{n%2B1}-u_n) a_{u_n}

converges.

Taking 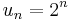u_n = 2^n, we see 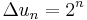\Delta u_n = 2^n, so the Cauchy condensation test emerges as a special case.

References

External links